MOE 2008.10

QuaSAR-Descriptor

---

Introduction

Default MOE descriptors were calculated based on single low energy conformers of the compounds. A detailed description of the interpretaton is given below:

2D Molecular Descriptors

2D molecular descriptors are defined to be numerical properties that can be calculated from the connection table representation of a molecule (e.g., elements, formal charges and bonds, but not atomic coordinates). 2D descriptors are, therefore, not dependent on the conformation of a molecule and are most suitable for large database studies.

Notation and Terminology

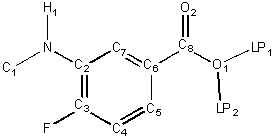
Many descriptors make use of several fundamental quantities that can be computed from a chemical structure. This section will define these fundamental quantities. For purposes of illustration, the following chemical structure will be used:

The fundamental quantities of a chemical structure depend solely on the structure as drawn, i.e., no modifications to the structure are implied with the exception of the addition or subtraction of hydrogen atoms to full valence.

Z denotes the atomic number of an atom; lone pair pseudo-atoms (LP) are given an atomic number of 0. Heavy atoms are atoms that have an atomic number strictly greater than 1 (not H nor LP). A trivial atom is an LP pseudo-atom or a hydrogen with exactly one heavy neighbor. In the reference structure, H₁, LP₁ and LP₂ are trivial.

The hydrogen count, h, of an atom is the number of hydrogens to which it is (or should be) attached. This count includes all hydrogen atoms that are necessary to fill valence. In the reference structure, F has h = 0, N has h = 1 and O₁ has h = 1.

The heavy degree, d, of an atom is the number of heavy atoms to which it is bonded. That is, d is the number of bonded neighbors of the atom in the hydrogen suppressed graph. In the reference structure, F has d = 1, C₆ has d = 3 and N has d = 2.

Physical Properties

The following physical properties can be calculated from the connection table (with no dependence on conformation) of a molecule:

Code	Description
apol	Sum of the atomic polarizabilities (including implicit hydrogens) with polarizabilities taken from [CRC 1994].
bpol	Sum of the absolute value of the difference between atomic polarizabilities of all bonded atoms in the molecule (including implicit hydrogens) with polarizabilities taken from [CRC 1994].
density	Molecular mass density: Weight divided by vdw_vol (amu/Å^3).
FCharge	Total charge of the molecule (sum of formal charges).
mr	Molecular refractivity (including implicit hydrogens). This property is calculated from an 11 descriptor linear model [MREF 1998] with r^2 = 0.997, RMSE = 0.168 on 1,947 small molecules.
SMR	Molecular refractivity (including implicit hydrogens). This property is an atomic contribution model [Crippen 1999] that assumes the correct protonation state (washed structures). The model was trained on ~7000 structures and results may vary from the mr descriptor.
Weight	Molecular weight (including implicit hydrogens) in atomic mass units with atomic weights taken from [CRC 1994].
logP(o/w)	Log of the octanol/water partition coefficient (including implicit hydrogens). This property is calculated from a linear atom type model [LOGP 1998] with r^2 = 0.931, RMSE=0.393 on 1,827 molecules.
logS	Log of the aqueous solubility (mol/L). This property is calculated from an atom contribution linear atom type model [Hou 2004] with r^2 = 0.90, ~1,200 molecules.
reactive	Indicator of the presence of reactive groups. A non-zero value indicates that the molecule contains a reactive group. The table of reactive groups is based on the Oprea set [Oprea 2000] and includes metals, phospho-, N/O/S-N/O/S single bonds, thiols, acyl halides, Michael Acceptors, azides, esters, etc.
SlogP	Log of the octanol/water partition coefficient (including implicit hydrogens). This property is an atomic contribution model [Crippen 1999] that calculates logP from the given structure; i.e., the correct protonation state (washed structures). Results may vary from the logP(o/w) descriptor. The training set for SlogP was ~7000 structures.
TPSA	Polar surface area (Å^2) calculated using group contributions to approximate the polar surface area from connection table information only. The parameterization is that of Ertl et al. [Ertl 2000].
vdw_vol	van der Waals volume (Å^3) calculated using a connection table approximation.
vdw_area	Area of van der Waals surface (Å^2) calculated using a connection table approximation.

Subdivided Surface Areas

The Subdivided Surface Areas are descriptors based on an approximate accessible van der Waals surface area (in Ų) calculation for each atom, v_i along with some other atomic property, p_i. The v_i are calculated using a connection table approximation. Each descriptor in a series is defined to be the sum of the v_i over all atoms i such that p_i is in a specified range (a,b).

In the descriptions to follow, L_i denotes the contribution to logP(o/w) for atom i as calculated in the SlogP descriptor [Crippen 1999]. R_i denotes the contribution to Molar Refractivity for atom i as calculated in the SMR descriptor [Crippen 1999]. The ranges were determined by percentile subdivision over a large collection of compounds.

Code	Description
SlogP_VSA0	Sum of vi such that Li <= -0.4.
SlogP_VSA1	Sum of vi such that Li is in (-0.4,-0.2].
SlogP_VSA2	Sum of vi such that Li is in (-0.2,0].
SlogP_VSA3	Sum of vi such that Li is in (0,0.1].
SlogP_VSA4	Sum of vi such that Li is in (0.1,0.15].
SlogP_VSA5	Sum of vi such that Li is in (0.15,0.20].
SlogP_VSA6	Sum of vi such that Li is in (0.20,0.25].
SlogP_VSA7	Sum of vi such that Li is in (0.25,0.30].
SlogP_VSA8	Sum of vi such that Li is in (0.30,0.40].
SlogP_VSA9	Sum of vi such that Li > 0.40.
SMR_VSA0	Sum of vi such that Ri is in [0,0.11].
SMR_VSA1	Sum of vi such that Ri is in (0.11,0.26].
SMR_VSA2	Sum of vi such that Ri is in (0.26,0.35].
SMR_VSA3	Sum of vi such that Ri is in (0.35,0.39].
SMR_VSA4	Sum of vi such that Ri is in (0.39,0.44].
SMR_VSA5	Sum of vi such that Ri is in (0.44,0.485].
SMR_VSA6	Sum of vi such that Ri is in (0.485,0.56].
SMR_VSA7	Sum of vi such that Ri > 0.56.

Atom Counts and Bond Counts

The atom count and bond count descriptors are functions of the counts of atoms and bonds (subdivided according to various criteria).

Code	Description
a_aro	Number of aromatic atoms.
a_count	Number of atoms (including implicit hydrogens). This is calculated as the sum of (1 + hi) over all non-trivial atoms i.
a_heavy	Number of heavy atoms #{Zi | Zi > 1}.
a_ICM	Atom information content (mean). This is the entropy of the element distribution in the molecule (including implicit hydrogens but not lone pair pseudo-atoms). Let ni be the number of occurrences of atomic number i in the molecule. Let pi = ni / n where n is the sum of the ni. The value of a_ICM is the negative of the sum over all i of pi log pi.
a_IC	Atom information content (total). This is calculated to be a_ICM times n.
a_nH	Number of hydrogen atoms (including implicit hydrogens). This is calculated as the sum of hi over all non-trivial atoms i plus the number of non-trivial hydrogen atoms.
a_nB	Number of boron atoms: #{Zi | Zi = 5}.
a_nC	Number of carbon atoms: #{Zi | Zi = 6}.
a_nN	Number of nitrogen atoms: #{Zi | Zi = 7}.
a_nO	Number of oxygen atoms: #{Zi | Zi = 8}.
a_nF	Number of fluorine atoms: #{Zi | Zi = 9}.
a_nP	Number of phosphorus atoms: #{Zi | Zi = 15}.
a_nS	Number of sulfur atoms: #{Zi | Zi = 16}.
a_nCl	Number of chlorine atoms: #{Zi | Zi = 17}.
a_nBr	Number of bromine atoms: #{Zi | Zi = 35}.
a_nI	Number of iodine atoms: #{Zi | Zi = 53}.
b_1rotN	Number of rotatable single bonds. Conjugated single bonds are not included (e.g., ester and peptide bonds).
b_1rotR	Fraction of rotatable single bonds: b_1rotN divided by b_heavy.
b_ar	Number of aromatic bonds.
b_count	Number of bonds (including implicit hydrogens). This is calculated as the sum of (di/2 + hi) over all non-trivial atoms i.
b_double	Number of double bonds. Aromatic bonds are not considered to be double bonds.
b_heavy	Number of bonds between heavy atoms.
b_rotN	Number of rotatable bonds. A bond is rotatable if it has order 1, is not in a ring, and has at least two heavy neighbors.
b_rotR	Fraction of rotatable bonds: b_rotN divided by b_heavy.
b_single	Number of single bonds (including implicit hydrogens). Aromatic bonds are not considered to be single bonds.
b_triple	Number of triple bonds. Aromatic bonds are not considered to be triple bonds.
chiral	The number of chiral centers.
chiral_u	The number of unconstrained chiral centers.
lip_acc	The number of O and N atoms.
lip_don	The number of OH and NH atoms.
lip_druglike	One if and only if lip_violation < 2 otherwise zero.
lip_violation	The number of violations of Lipinski's Rule of Five [Lipinski 1997].
nmol	The number of molecules (connected components).
opr_brigid	The number of rigid bonds from [Oprea 2000].
opr_leadlike	One if and only if opr_violation < 2 otherwise zero.
opr_nring	The number of ring bonds from [Oprea 2000].
opr_nrot	The number of rotatable bonds from [Oprea 2000].
opr_violation	The number of violations of Oprea's lead-like test [Oprea 2000].
rings	The number of rings.
VAdjMa	Vertex adjacency information (magnitude): 1 + log2 m where m is the number of heavy-heavy bonds. If m is zero, then zero is returned.
VAdjEq	Vertex adjacency information (equality): -(1-f)log2(1-f) - f log2 f where f = (n^2 - m) / n^2, n is the number of heavy atoms and m is the number of heavy-heavy bonds. If f is not in the open interval (0,1), then 0 is returned.

Kier&Hall Connectivity and Kappa Shape Indices

For a heavy atom i let v_i = (p_i - h_i) / (Z_i - p_i - 1) where p_i is the number of s and p valence electrons of atom i. The Kier and Hall chi connectivity indices are calculated from the heavy atom degree d_i (number of heavy neighbors) and v_i. The Kier and Hall kappa molecular shape indices [Hall 1991] compare the molecular graph with minimal and maximal molecular graphs, and are intended to capture different aspects of molecular shape. In the following description, n denotes the number of atoms in the hydrogen suppressed graph, m is the number of bonds in the hydrogen suppressed graph and a is the sum of (r_i/r_c - 1) where r_i is the covalent radius of atom i, and r_c is the covalent radius of a carbon atom. Also, let p₂ denote the number of paths of length 2 and p₃ the number of paths of length 3.

Code	Description
chi0	Atomic connectivity index (order 0) from [Hall 1991] and [Hall 1977]. This is calculated as the sum of 1/sqrt(di) over all heavy atoms i with di > 0.
chi0_C	Carbon connectivity index (order 0). This is calculated as the sum of 1/sqrt(di) over all carbon atoms i with di > 0.
chi1	Atomic connectivity index (order 1) from [Hall 1991] and [Hall 1977]. This is calculated as the sum of 1/sqrt(didj) over all bonds between heavy atoms i and j where i < j.
chi1_C	Carbon connectivity index (order 1). This is calculated as the sum of 1/sqrt(didj) over all bonds between carbon atoms i and j where i < j.
chi0v	Atomic valence connectivity index (order 0) from [Hall 1991] and [Hall 1977]. This is calculated as the sum of 1/sqrt(vi) over all heavy atoms i with vi > 0.
chi0v_C	Carbon valence connectivity index (order 0). This is calculated as the sum of 1/sqrt(vi) over all carbon atoms i with vi > 0.
chi1v	Atomic valence connectivity index (order 1) from [Hall 1991] and [Hall 1977]. This is calculated as the sum of 1/sqrt(vivj) over all bonds between heavy atoms i and j where i < j.
chi1v_C	Carbon valence connectivity index (order 1). This is calculated as the sum of 1/sqrt(vivj) over all bonds between carbon atoms i and j where i < j.
Kier1	First kappa shape index: (n-1)^2 / m^2 [Hall 1991].
Kier2	Second kappa shape index: (n-1)^2 / m^2 [Hall 1991].
Kier3	Third kappa shape index: (n-1) (n-3)^2 / p3^2 for odd n, and (n-3) (n-2)^2 / p3^2 for even n [Hall 1991].
KierA1	First alpha modified shape index: s (s-1)^2 / m^2 where s = n + a [Hall 1991].
KierA2	Second alpha modified shape index: s (s-1)^2 / m^2 where s = n + a [Hall 1991].
KierA3	Third alpha modified shape index: (n-1) (n-3)^2 / p3^2 for odd n, and (n-3) (n-2)^2 / p3^2 for even n where s = n + a [Hall 1991].
KierFlex	Kier molecular flexibility index: (KierA1) (KierA2) / n [Hall 1991].
zagreb	Zagreb index: the sum of di^2 over all heavy atoms i.

Adjacency and Distance Matrix Descriptors

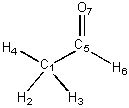
The adjacency matrix, M, of a chemical structure is defined by the elements [M_ij] where M_ij is 1 if atoms i and j are bonded and zero otherwise. The distance matrix, D, of a chemical structure is defined by the elements [D_ij] where D_ij is the length of the shortest path from atoms i to j; zero is used if atoms i and j are not part of the same connected component. The adjacency matrix of CH3CH=O is displayed on the left and its distance matrix is displayed on the right (below):

C1 0 1 1 1 1 0 0 0 1 1 1 1 2 2 H2 1 0 0 0 0 0 0 1 0 2 2 2 3 3 H3 1 0 0 0 0 0 0 1 2 0 2 2 3 3 H4 1 0 0 0 0 0 0 1 2 2 0 2 3 3 C5 1 0 0 0 0 1 1 1 2 2 2 0 1 1 H6 0 0 0 0 1 0 0 2 3 3 3 1 0 2 O7 0 0 0 0 1 0 0 2 3 3 3 1 2 0

Petitjean [Petitjean 1992] defines the eccentricity of a vertex to be the longest path from that vertex to any other vertex in the graph. The graph radius is the smallest vertex eccentricity in the graph and the graph diameter as the largest vertex eccentricity. These values are calculated using the distance matrix and are used for several descriptors described below.

The following descriptors are calculated from the distance and adjacency matrices of the heavy atoms:

Code	Description
balabanJ	Balaban's connectivity topological index [Balaban 1982].
BCUT_PEOE_0 BCUT_PEOE_1 BCUT_PEOE_2 BCUT_PEOE_3	The BCUT descriptors [Pearlman 1998] are calculated from the eigenvalues of a modified adjacency matrix. Each ij entry of the adjacency matrix takes the value 1/sqrt(bij) where bij is the formal bond order between bonded atoms i and j. The diagonal takes the value of the PEOE partial charges. The resulting eigenvalues are sorted and the smallest, 1/3-ile, 2/3-ile and largest eigenvalues are reported.
BCUT_SLOGP_0 BCUT_SLOGP_1 BCUT_SLOGP_2 BCUT_SLOGP_3	The BCUT descriptors using atomic contribution to logP (using the Wildman and Crippen SlogP method) instead of partial charge.
BCUT_SMR_0 BCUT_SMR_1 BCUT_SMR_2 BCUT_SMR_3	The BCUT descriptors using atomic contribution to molar refractivity (using the Wildman and Crippen SMR method) instead of partial charge.
diameter	Largest value in the distance matrix [Petitjean 1992].
petitjean	Value of (diameter - radius) / diameter.
GCUT_PEOE_0 GCUT_PEOE_1 GCUT_PEOE_2 GCUT_PEOE_3	The GCUT descriptors are calculated from the eigenvalues of a modified graph distance adjacency matrix. Each ij entry of the adjacency matrix takes the value 1/sqr(dij) where dij is the (modified) graph distance between atoms i and j. The diagonal takes the value of the PEOE partial charges. The resulting eigenvalues are sorted and the smallest, 1/3-ile, 2/3-ile and largest eigenvalues are reported.
GCUT_SLOGP_0 GCUT_SLOGP_1 GCUT_SLOGP_2 GCUT_SLOGP_3	The GCUT descriptors using atomic contribution to logP (using the Wildman and Crippen SlogP method) instead of partial charge.
GCUT_SMR_0 GCUT_SMR_1 GCUT_SMR_2 GCUT_SMR_3	The GCUT descriptors using atomic contribution to molar refractivity (using the Wildman and Crippen SMR method) instead of partial charge.
petitjeanSC	Petitjean graph Shape Coefficient as defined in [Petitjean 1992]: (diameter - radius) / radius.
radius	If ri is the largest matrix entry in row i of the distance matrix D, then the radius is defined as the smallest of the ri [Petitjean 1992].
VDistEq	If m is the sum of the distance matrix entries then VdistEq is defined to be the sum of log2 m - pi log2 pi / m where pi is the number of distance matrix entries equal to i.
VDistMa	If m is the sum of the distance matrix entries then VDistMa is defined to be the sum of log2 m - Dij log2 Dij / m over all i and j.
wienerPath	Wiener path number: half the sum of all the distance matrix entries as defined in [Balaban 1979] and [Wiener 1947].
wienerPol	Wiener polarity number: half the sum of all the distance matrix entries with a value of 3 as defined in [Balaban 1979].

Pharmacophore Feature Descriptors

The Pharmacophore Atom Type descriptors consider only the heavy atoms of a molecule and assign a type to each atom. That is, hydrogens are suppressed during the calculation. The atom typing mechanism is located in the file $MOE/lib/svl/ph4.svl/ph4type.svl which is a rule-based system for assigning pharmacophore features to atoms. The feature set is Donor, Acceptor, Polar (both Donor and Acceptor), Positive (base), Negative (acid), Hydrophobe and Other. Assignments may take into account implied protonation, deprotonation, keto/enol considerations and tautomerism at a biologically relevant pH. For example, -COOH will be typed in its deprotonated form regardless of how the structure is stored.

Code	Description
a_acc	Number of hydrogen bond acceptor atoms (not counting acidic atoms but counting atoms that are both hydrogen bond donors and acceptors such as -OH).
a_acid	Number of acidic atoms.
a_base	Number of basic atoms.
a_don	Number of hydrogen bond donor atoms (not counting basic atoms but counting atoms that are both hydrogen bond donors and acceptors such as -OH).
a_hyd	Number of hydrophobic atoms.
vsa_acc	Approximation to the sum of VDW surface areas (Å^2) of pure hydrogen bond acceptors (not counting acidic atoms and atoms that are both hydrogen bond donors and acceptors such as -OH).
vsa_acid	Approximation to the sum of VDW surface areas of acidic atoms (Å^2).
vsa_base	Approximation to the sum of VDW surface areas of basic atoms (Å^2).
vsa_don	Approximation to the sum of VDW surface areas of pure hydrogen bond donors (not counting basic atoms and atoms that are both hydrogen bond donors and acceptors such as -OH) (Å^2).
vsa_hyd	Approximation to the sum of VDW surface areas of hydrophobic atoms (Å^2).
vsa_other	Approximation to the sum of VDW surface areas (Å^2) of atoms typed as "other".
vsa_pol	Approximation to the sum of VDW surface areas (Å^2) of polar atoms (atoms that are both hydrogen bond donors and acceptors), such as -OH.

Partial Charge Descriptors

Descriptors that depend on the partial charge of each atom of a chemical structure require calculation of those partial charges. An unfortunate complication is the fact that there are numerous methods of calculating partial charges. Rather than enforce a particular method, MOE provides several versions of most of the charge-dependent descriptors. The only difference between these variants is the source of the partial charges. The following variants are supported: PEOE, Q (described below).

PEOE. The Partial Equalization of Orbital Electronegativities (PEOE) method of calculating atomic partial charges [Gasteiger 1980] is a method in which charge is transferred between bonded atoms until equilibrium. To guarantee convergence, the amount of charge transferred at each iteration is damped with an exponentially decreasing scale factor. The amount of charge transferred, dq_ij, between atoms i and j when X_i > X_j is

dq_ij = (1/2^k) (X_i - X_j) / X_j⁺

where X_j⁺ is the electronegativity of the positive ion of atom j; X_i is the electronegativity of atom i (quadratically dependent on partial charge); and k is the iteration number of the algorithm. Electronegativity values are determined by parameterization found in the SVL source code file $MOE/lib/svl/calc.svl/charge.svl. The PEOE charges depend only on the connectivity of the input structures: elements, formal charges and bond orders. Descriptors using the PEOE charges are prefixed with PEOE_.

Q. Descriptors prefixed with Q_ use the partial charges stored with each structure in the database. In other words, no partial charge calculation is made and it is assumed that some external program has been used to calculate the atomic partial charges. This dependence can be a subtle source of error if, for example, the wrong charges are stored when descriptors are recalculated (e.g., when evaluating QSAR models on novel structures).

Let q_i denote the partial charge of atom i as defined above. Let v_i be the van der Waals surface area (Ų) of atom i (as calculated by a connection table approximation). The following descriptors are calculated:

Code	Description
Q_PC+ PEOE_PC+	Total positive partial charge: the sum of the positive qi. Q_PC+ is identical to PC+ which has been retained for compatibility.
Q_PC- PEOE_PC-	Total negative partial charge: the sum of the negative qi. Q_PC- is identical to PC- which has been retained for compatibility.
Q_RPC+ PEOE_RPC+	Relative positive partial charge: the largest positive qi divided by the sum of the positive qi. Q_RPC+ is identical to RPC+ which has been retained for compatibility.
Q_PRC- PEOE_RPC-	Relative negative partial charge: the smallest negative qi divided by the sum of the negative qi. Q_RPC- is identical to RPC- which has been retained for compatibility.
Q_VSA_POS PEOE_VSA_POS	Total positive van der Waals surface area. This is the sum of the vi such that qi is non-negative. The vi are calculated using a connection table approximation.
Q_VSA_NEG PEOE_VSA_NEG	Total negative van der Waals surface area. This is the sum of the vi such that qi is negative. The vi are calculated using a connection table approximation.
Q_VSA_PPOS PEOE_VSA_PPOS	Total positive polar van der Waals surface area. This is the sum of the vi such that qi is greater than 0.2. The vi are calculated using a connection table approximation.
Q_VSA_PNEG PEOE_VSA_PNEG	Total negative polar van der Waals surface area. This is the sum of the vi such that qi is less than -0.2. The vi are calculated using a connection table approximation.
Q_VSA_HYD PEOE_VSA_HYD	Total hydrophobic van der Waals surface area. This is the sum of the vi such that |qi| is less than or equal to 0.2. The vi are calculated using a connection table approximation.
Q_VSA_POL PEOE_VSA_POL	Total polar van der Waals surface area. This is the sum of the vi such that |qi| is greater than 0.2. The vi are calculated using a connection table approximation.
Q_VSA_FPOS PEOE_VSA_FPOS	Fractional positive van der Waals surface area. This is the sum of the vi such that qi is non-negative divided by the total surface area. The vi are calculated using a connection table approximation.
Q_VSA_FNEG PEOE_VSA_FNEG	Fractional negative van der Waals surface area. This is the sum of the vi such that qi is negative divided by the total surface area. The vi are calculated using a connection table approximation.
Q_VSA_FPPOS PEOE_VSA_FPPOS	Fractional positive polar van der Waals surface area. This is the sum of the vi such that qi is greater than 0.2 divided by the total surface area. The vi are calculated using a connection table approximation.
Q_VSA_FPNEG PEOE_VSA_FPNEG	Fractional negative polar van der Waals surface area. This is the sum of the vi such that qi is less than -0.2 divided by the total surface area. The vi are calculated using a connection table approximation.
Q_VSA_FHYD PEOE_VSA_FHYD	Fractional hydrophobic van der Waals surface area. This is the sum of the vi such that |qi| is less than or equal to 0.2 divided by the total surface area. The vi are calculated using a connection table approximation.
Q_VSA_FPOL PEOE_VSA_FPOL	Fractional polar van der Waals surface area. This is the sum of the vi such that |qi| is greater than 0.2 divided by the total surface area. The vi are calculated using a connection table approximation.
PEOE_VSA+6	Sum of vi where qi is greater than 0.3.
PEOE_VSA+5	Sum of vi where qi is in the range [0.25,0.30).
PEOE_VSA+4	Sum of vi where qi is in the range [0.20,0.25).
PEOE_VSA+3	Sum of vi where qi is in the range [0.15,0.20).
PEOE_VSA+2	Sum of vi where qi is in the range [0.10,0.15).
PEOE_VSA+1	Sum of vi where qi is in the range [0.05,0.10).
PEOE_VSA+0	Sum of vi where qi is in the range [0.00,0.05).
PEOE_VSA-0	Sum of vi where qi is in the range [-0.05,0.00).
PEOE_VSA-1	Sum of vi where qi is in the range [-0.10,-0.05).
PEOE_VSA-2	Sum of vi where qi is in the range [-0.15,-0.10).
PEOE_VSA-3	Sum of vi where qi is in the range [-0.20,-0.15).
PEOE_VSA-4	Sum of vi where qi is in the range [-0.25,-0.20).
PEOE_VSA-5	Sum of vi where qi is in the range [-0.30,-0.25).
PEOE_VSA-6	Sum of vi where qi is less than -0.30.

3D Molecular Descriptors

There are two types of 3D molecular descriptors: those that depend on internal coordinates only and those that depend on absolute orientation. 3D molecular descriptors are classified as "i3D" for internal coordinate dependent 3D and "x3D" for external coordinate dependent. A good example is the dipole moment: the magnitude of the dipole moment does not depend on absolute orientation in space; however, the x component of the dipole moment does depend on absolute orientation.

Note: All the 3D descriptors operate on structures found in the database as is; that is, no hydrogens are added or removed. Furthermore, most descriptors assume that partial charges are stored with the structures in the database.

MOPAC Descriptors

The MOPAC [MOPAC] descriptors are calculated by the version of MOPAC6 distributed with MOE.

Code	Description
AM1_dipole	The dipole moment calculated using the AM1 Hamiltonian [MOPAC].
AM1_E	The total energy (kcal/mol) calculated using the AM1 Hamiltonian [MOPAC].
AM1_Eele	The electronic energy (kcal/mol) calculated using the AM1 Hamiltonian [MOPAC].
AM1_HF	The heat of formation (kcal/mol) calculated using the AM1 Hamiltonian [MOPAC].
AM1_IP	The ionization potential (kcal/mol) calculated using the AM1 Hamiltonian [MOPAC].
AM1_LUMO	The energy (eV) of the Lowest Unoccupied Molecular Orbital calculated using the AM1 Hamiltonian [MOPAC].
AM1_HOMO	The energy (eV) of the Highest Occupied Molecular Orbital calculated using the AM1 Hamiltonian [MOPAC].
MNDO_dipole	The dipole moment calculated using the MNDO Hamiltonian [MOPAC].
MNDO_E	The total energy (kcal/mol) calculated using the MNDO Hamiltonian [MOPAC].
MNDO_Eele	The electronic energy (kcal/mol) calculated using the MNDO Hamiltonian [MOPAC].
MNDO_HF	The heat of formation (kcal/mol) calculated using the MNDO Hamiltonian [MOPAC].
MNDO_IP	The ionization potential (kcal/mol) calculated using the MNDO Hamiltonian [MOPAC].
MNDO_LUMO	The energy (eV) of the Lowest Unoccupied Molecular Orbital calculated using the MNDO Hamiltonian [MOPAC].
MNDO_HOMO	The energy (eV) of the Highest Occupied Molecular Orbital calculated using the MNDO Hamiltonian [MOPAC].
PM3_dipole	The dipole moment calculated using the PM3 Hamiltonian [MOPAC].
PM3_E	The total energy (kcal/mol) calculated using the PM3 Hamiltonian [MOPAC].
PM3_Eele	The electronic energy (kcal/mol) calculated using the PM3 Hamiltonian [MOPAC].
PM3_HF	The heat of formation (kcal/mol) calculated using the PM3 Hamiltonian [MOPAC].
PM3_IP	The ionization potential (kcal/mol) calculated using the PM3 Hamiltonian [MOPAC].
PM3_LUMO	The energy (eV) of the Lowest Unoccupied Molecular Orbital calculated using the PM3 Hamiltonian [MOPAC].
PM3_HOMO	The energy (eV) of the Highest Occupied Molecular Orbital calculated using the PM3 Hamiltonian [MOPAC].

Surface Area, Volume and Shape Descriptors

The following descriptors depend on the structure connectivity and conformation (dimensions are measured in Å). The vsurf_ descriptors are similar to the VolSurf descriptors [Cruciani 2000]; these descriptors have been shown to be useful in pharmacokinetic property prediction.

Code	Description
ASA	Water accessible surface area calculated using a radius of 1.4 A for the water molecule. A polyhedral representation is used for each atom in calculating the surface area.
dens	Mass density: molecular weight divided by van der Waals volume as calculated in the vol descriptor.
glob	Globularity, or inverse condition number (smallest eigenvalue divided by the largest eigenvalue) of the covariance matrix of atomic coordinates. A value of 1 indicates a perfect sphere while a value of 0 indicates a two- or one-dimensional object.
pmi	Principal moment of inertia.
pmiX	x component of the principal moment of inertia (external coordinates).
pmiY	y component of the principal moment of inertia (external coordinates).
pmiZ	z component of the principal moment of inertia (external coordinates).
rgyr	Radius of gyration.
std_dim1	Standard dimension 1: the square root of the largest eigenvalue of the covariance matrix of the atomic coordinates. A standard dimension is equivalent to the standard deviation along a principal component axis.
std_dim2	Standard dimension 2: the square root of the second largest eigenvalue of the covariance matrix of the atomic coordinates. A standard dimension is equivalent to the standard deviation along a principal component axis.
std_dim3	Standard dimension 3: the square root of the third largest eigenvalue of the covariance matrix of the atomic coordinates. A standard dimension is equivalent to the standard deviation along a principal component axis.
vol	van der Waals volume calculated using a grid approximation (spacing 0.75 A).
VSA	van der Waals surface area. A polyhedral representation is used for each atom in calculating the surface area.
vsurf_V	Interaction field volume
vsurf_S	Interaction field surface area
vsurf_S	Surface rugosity
vsurf_S	Surface globularity
vsurf_W*	Hydrophilic volume (8 descriptors)
vsurf_IW*	Hydrophilic integy moment (8 descriptors)
vsurf_CW*	Capacity factor (8 descriptors)
vsurf_EWmin*	Lowest hydrophilic energy (3 descriptors)
vsurf_DW*	Contact distances of vsurf_EWmin (3 descriptors)
vsurf_D*	Hydrophobic volume (8 descriptors)
vsurf_ID*	Hydrophobic integy moment (8 descriptors)
vsurf_EDmin*	Lowest hydrophobic energy (3 descriptors)
vsurf_DD*	Contact distances of vsurf_DDmin (3 descriptors)
vsurf_HL*	Hydrophilic-Lipophilic (2 descriptors)
vsurf_A	Amphiphilic moment
vsurf_CA	Critical packing parameter
vsurf_Wp*	Polar volume (8 descriptors)
vsurf_HB1*	H-bond donor capacity (8 descriptors)

Conformation Dependent Charge Descriptors

The following descriptors depend upon the stored partial charges of the molecules and their conformations. Accessible surface area refers to the water accessible surface (in Ų) area using a probe radius of 1.4 Å. Let q_i denote the partial charge of atom i.

Code	Description
ASA+	Water accessible surface area of all atoms with positive partial charge (strictly greater than 0).
ASA-	Water accessible surface area of all atoms with negative partial charge (strictly less than 0).
ASA_H	Water accessible surface area of all hydrophobic (|qi|<0.2) atoms.
ASA_P	Water accessible surface area of all polar (|qi|>=0.2) atoms.
DASA	Absolute value of the difference between ASA+ and ASA-.
CASA+	Positive charge weighted surface area, ASA+ times max { qi > 0 } [Stanton 1990].
CASA-	Negative charge weighted surface area, ASA- times max { qi < 0 } [Stanton 1990].
DCASA	Absolute value of the difference between CASA+ and CASA- [Stanton 1990].
dipole	Dipole moment calculated from the partial charges of the molecule.
dipoleX	The x component of the dipole moment (external coordinates).
dipoleY	The y component of the dipole moment (external coordinates).
dipoleZ	The z component of the dipole moment (external coordinates).
FASA+	Fractional ASA+ calculated as ASA+ / ASA.
FASA-	Fractional ASA- calculated as ASA- / ASA.
FCASA+	Fractional CASA+ calculated as CASA+ / ASA.
FCASA-	Fractional CASA- calculated as CASA- / ASA.
FASA_H	Fractional ASA_H calculated as ASA_H / ASA.
FASA_P	Fractional ASA_P calculated as ASA_P / ASA.

References

[Balaban 1979]	Balaban, A.T.; Five New Topological Indices for the Branching of Tree-Like Graphs; Theoretica Chimica Acta 53 (1979) 355–375.
[Balaban 1982]	Balaban, A.T.; Highly Discriminating Distance-Based Topological Index; Chemical Physics Letters 89 No. 5 (1982) 399–404.
[CRC 1994]	CRC Handbook of Chemistry and Physics. CRC Press (1994).
[Crippen 1999]	Wildman, S.A., Crippen, G.M.; Prediction of Physiochemical Parameters by Atomic Contributions; J. Chem. Inf. Comput. Sci. 39 No. 5 (1999) 868–873.
[Cruciani 2000]	Cruciani, G., Crivori, P., Carrupt, P.-A., Testa, B.; Molecular Fields in Quantitative Structure-Permeation Relationships: the VolSurf Approach; J. Mol. Struct. (Theochem) 503 (2000) 17–30.
[Gasteiger 1980]	Gasteiger, J., Marsili, M.; Iterative Partial Equalization of Orbital Electronegativity - A Rapid Access to Atomic Charges; Tetrahedron 36 (1980) 3219.
[Ertl 2000]	Ertl, P., Rohde, B., Selzer, P.; Fast Calculation of Molecular Polar Surface Area as a Sum of Fragment-Based Contributions and Its Application to the Prediction of Drug Transport Properties; J. Med. Chem. 43 (2000) 3714–3717.
[Hall 1991]	Hall, L.H., Kier, L.B.; The Molecular Connectivity Chi Indices and Kappa Shape Indices in Structure-Property Modeling; Reviews of Computational Chemistry 2 (1991).
[Hall 1977]	Hall, L.H., Kier, L.B.; The Nature of Structure-Activity Relationships and Their Relation to Molecular Connectivity; Eur. J. Med. Chem 12 (1977) 307.
[Hou 2004]	Hou, T.J., Xia, K., Zhang, W., Xu, X.J.; ADME Evaluation in Drug Discovery. 4. Prediction of Aqueous Solubility Based on Atom Contribution Approach; J. Chem. Inf. Comput. Sci. 44 (2004) 266–275.
[Lipinski 1997]	Lipinski, C.A., Lombardo, F., Dominy, B.W. and Feeney, P.J.; Experimental and Computational Approaches to Estimate Solubility and Permeability in Drug Discovery and Development Settings; Adv. Drug Deliv. Rev. 23 (1997) 3–25.
[LOGP 1998]	Labute, P.; MOE LogP(Octanol/Water) Model unpublished. Source code in $MOE/lib/svl/quasar.svl/q_logp.svl (1998).
[MOPAC]	Stewart, J.J.P.; MOPAC Manual (Seventh Edition); 1993.
[MREF 1998]	Labute, P.; MOE Molar Refractivity Model unpublished. Source code in $MOE/lib/svl/quasar.svl/q_mref.svl (1998).
[Oprea 2000]	Oprea, Tudor I.; Property Distribution of Drug-Related Chemical Databases; J. Comp. Aid. Mol. Des. 14 (2000) 251–264.
[Pearlman 1998]	Pearlman, R.S., Smith, K.M.; Novel Software Tools for Chemical Diversity; Persp. Drug. Disc. Des. 9/10/11 (1998) 339–353.
[Petitjean 1992]	Petitjean, M.; Applications of the Radius-Diameter Diagram to the Classification of Topological and Geometrical Shapes of Chemical Compounds; J. Chem. Inf. Comput. Sci. 32 (1992) 331–337.
[Stanton 1990]	Stanton, D., Jurs, P.; Development and Use of Charged Partial Surface-Area Structural Descriptors in Computer-Assisted Quantitative Structure-Property Relationship Studies; Anal. Chem. 62 (1990) 2323–2329.
[Wiener 1947]	Wiener, H.; Structural Determination of Paraffin Boiling Points; Journal of the American Chemical Society 69 (1947) 17–20.

---

Copyright © 1997-2008 Chemical Computing Group Inc.
info@chemcomp.com